I have conducted a number of research projects related to Signal Detection Theory.
Decision Noise
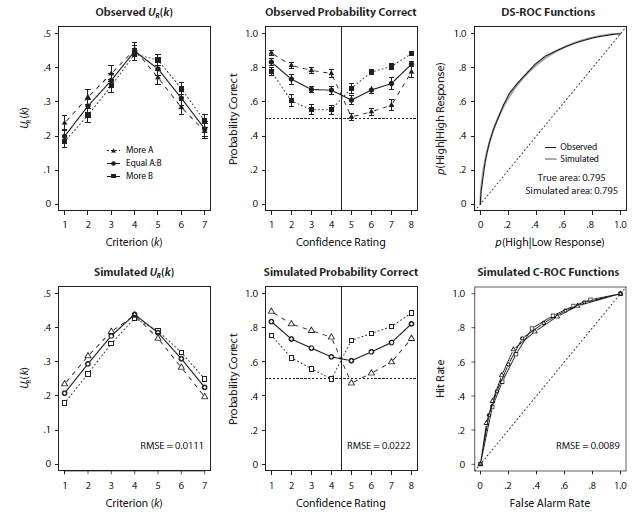
Decision Noise. Standard implementations of signal detection theory attributes all noise to perceptual processes. I have developed the Decision Noise Model (DNM), a modification of Signal Detection Theory that incorporates noise into the response process as well. The DNM illustrates how inconsistencies in the response can produce ROC functions that violate the assumptions of SDT, but that others have argued point out a fundamental inadequacy of that theory. This claim led to a published critique of our paper which we responded to here. The paper also introduces and discusses a novel ROC analysis we called the DS-ROC function that can help measure the influence of perceptual processes in signal detection tasks. DS-ROC can be a useful way to make an ROC function when you have measureable noise in the stimulus, but want to avoid the problems and complications with confidence ratings.
Non-Parametric Measures of Sensitivity
Standard measures of sensitivity and bias in signal detection theory rely on assumptions about signal and noise distributions. As an alternative, researchers have sometimes used the ‘non-parametric’ measure A’ (a-prime), which does not rely on the same types of distribution-based assumptions. In truth, it is probably usually used because it is still defined, even when you have 100% or 0% hits/false alarms. Yet even though A’ is commonly used, it does not measure what most people using it have claimed it measures (which is the average between the minimum and maximum ROC functions that can pass through a point).